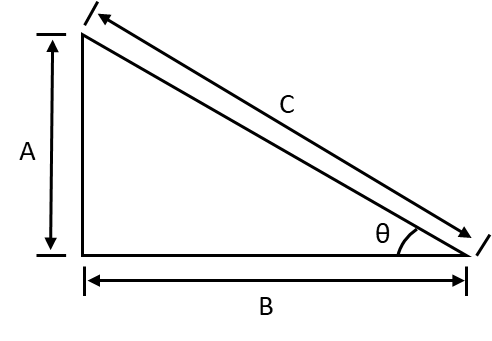
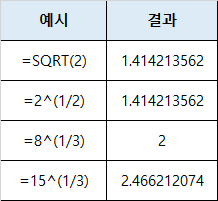
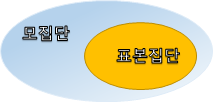
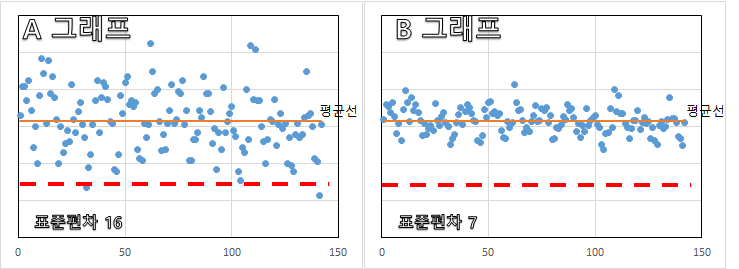
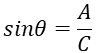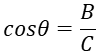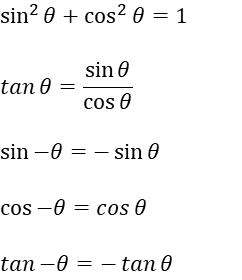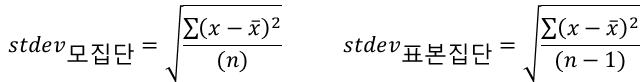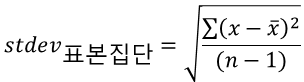삼각함수의 사용하는 예에 대해서 소개하려고합니다.

기하학에서는 아주 오래 전 부터 삼각 측량법(Triangulation Surveying)으로 위치를 파악해 왔습니다.

오래되었고 기본적이지만 조건만 맞으면 아주 정확합니다.

1. 삼각 측량법 사용

A와 B를 정확하게 알고 있을 때 관측된 C의 위치를 계산합니다.

A와 B에서 관측하여 각도 ∠CAB(α)와 ∠ABC( β )를 측정합니다.

삼각형 △ABC는 보통은 직각삼각형이 아닙니다.

그래서 직사각형을 만드는 D를 먼저 만들어 알아내야 합니다.

먼저 삼각형의 내각의 합은 180˚가 되니  ∠ACB( γ )를 구할 수 있습니다.

그럼 사인법칙이 사용할 수 있습니다.

사인 법칙을 활용해서 거리를 AC의 거리를 알아냈습니다.

이제 AD를 알아내겠습니다.

이제 AC와 AD를 다 구했습니다.

피타코라스 법칙으로 DC를 구하면 C의 위치를 구한 것입니다.

2. 산의 높이 구하기

이번에는 산의 높이를 측정한다고 치겠습니다.
먼저 산 아래에서 정확한 두점의 위치를 찍습니다.
그리고 산꼭대기를 보면 기울어진 삼각형을 만들수가 있죠.

① 직각이 되는위의 방법과 같이 위치 D를 만들고 CD의 길이를 구합니다. 

② D로 이동하여 다시 C까지의 각도 "??"를 측정합니다.(관측을 2번)

그럼 CD의 길이와 각도 ??를 알고 있습니다.

산의 높이(CE) = CD * sin ?? 가 됩니다.

3. 삼각측량법의 응용

위의 원리를 이용해서 여러 개의 중개탑을 설치해서 여러 위치를 관측합니다.

그럼 이 데이터들로 연결해서 많은 삼각형을 만들수 있습니다.

이걸 이용해서 이 안의 거리를 구하는 방식으로 어디든 위치를 알 수 있습니다.

그래도 측량에는 사실 오차가 조금 있습니다.

이 때 한개의 위치를 여러개의 신호탑에서 삼각 계측법을 사용해서 위치의 정밀도를 높입니다.

복잡한 망을 만들어 위치를 정밀하게 파악하는 네비게이션도 사실 근본적으로는 삼각 계측법을 다중으로 전개합니다.

지구가 둥글기 때문에 넓은 거리를 이동할 때는 보완하는 계산이 따로 필요하기는 합니다.

기술이 발달함에 따라 초단위의 각도변화도 계산할 수 있어 별의 거리도 측정하고는 합니다.

단순하지만 강력한 거리 파악법인 삼각 측량법은 현대에서도 널리 쓰이고 있습니다.

아직도 추가적인 활용법이 연구되고 있다고 하니 간단한 아이디어가 얼마나 힘이 있는지 알 수 있습니다.

과학에 대해서 공부하다보면 이게 진짜로 되느냐 고민할 때가 많습니다.

그 중 중요한건 형상이 나오느냐로 기하에 대한 내용입니다.

물건의 형상에 대해서 공부할때 가장 먼저 나오는 삼각비와 삼각함수에 대해서 알아보겠습니다.

학교에서 배우는 공식이나 계산 테크닉이 아니라 의미에 대해서 포스팅 했습니다.

1. 삼각비

세 변과 세 각을 가진 도형을 삼각형이라고하고, 그중에서 한각을 직각으로 삼는 삼각형을 직각삼각형이라고 합니다.

이 직각 삼각형은 각도중에 하나가 고정됨에 각 변들이 사이에 관계가 생깁니다.

직각 삼각형의 두개 성분의 비를 삼각비라고 합니다.

그야말로 기하학의 기초인 삼각비는 농경이 발달한 서아시아, 인도, 이슬람 세계에서 발전했습니다.
이 유서깊은 삼각함수는 가장 대표적인 것은 3개로,

• 사인 - sin : 기준각으로부터 마주보는 변(맞변)과 빗변의 비
  
• 코사인 - cos : 기준각을 포함하는 변(밑변)과 빗변의 비 
  
• 탄젠트 - tan : 기준각을 마주보는 변(맞변)과 기준각을 포함하는 변(밑변)의 비 
  

잘 사용하지는 않지만 각 함수의 역수개념으로 cosecant, secant, cotangent 가 있습니다.

cosecant = csc θ = 1/sin θ, secant θ = sec θ = 1/cos θ, cotangent = cot θ = 1/tan θ 입니다.

직각삼각형의 경우, 0도와 90도가 되는 값은 정의할 수가 없습니다. 그릴수가 없으니까요.

하지만 아래와 같이 정의하는 것이 가능합니다.

2. 삼각함수

삼각비와 삼각함수를 같은 것으로 생각할 수 있지만, 대상이 되는 구간이 다릅니다.

이런 관계를 정의역이 다르다라고 할 수 있습니다. 

삼각비는 0˚ ~ 90˚까지 계산이 가능하지만, 삼각함수는 0˚ ~ 360˚까지 확장한 개념입니다.

즉 직각삼각형의 비에서 출발하기는 했지만 전 각도에 다 성립하는 구간입니다.

수치적으로는 무한급수로 성립하는 공식을 보면 아래와 같습니다.

이때 θ는 radian 단위입니다.

삼각함수는 거의 모든 계산기나 수치계산 프로그램이라면 기본적으로 다 계산해줍니다.

이런식으로 형성되는 것만 봐두면 됩니다.

이렇게 정의 되는 삼각함수의 가장 큰 특성은 파동성입니다.
어떤 값으로 나아가는게 아닌 주기를 가지고 같은 모양이 반복되고, 같은 숫자가 다시 나옵니다.
세상에는 많은 물리특성들이 파동성을 가지고 있기 때문에 표현식으로 삼각함수를 많이 활용합니다.

사실 공식을 가능하면 안외우고 가고 싶은데, 그래도 어느정도는 알아두어야 합니다.

기하학의 가장 원천 공식인 만큼 계산하는 솔루션이 많고 실제 공식도 다양합니다.

학생이라면 학교에서 배우고 문제를 풀게 되겠죠.

알아 두었으면 하는 삼각함수의 관계에 대한 주요공식은 아래와 같습니다.

공식에 대해서 다룰때는 사용법에 대해서 고민하고, 포스팅하려고 노력합니다.

하지만 어떨때는 이론 그자체를 다뤄야 할 때도 있습니다.

오늘은 삼각함수가 무엇인지 그 자체에 대해서 알아봤는데요.

앞으로 이 걸 사용해서 할 수 있는 일들도 조금씩 풀어 나갔으면 좋겠습니다.

"각"이라는 건 두 선이 만나는 벌어진 정도를 말합니다. 

이 각을 값으로 나타내어 수치화 한 것이 "각도"입니다.

각도에는 원을 360도로 나타내어 직각은 90도로 나타내는 도 단위가 가장 흔한 단위입니다.

1도는 1˚라고 쓰는 가장 기본적인 단위입니다.

각도에는 여러가지 가설이 있지만, 고대 로마인들이 1년을 360일로 생각할 때 결정된 것 같습니다.

태양의 변화주기가 원형인 것을 생각해 정했다고 합니다.

그리고 진행방향을 기준으로 오른쪽을 3시, 왼쪽을 9시로 하는 시간으로 나타내는 방법이 있습니다.

시계의 시간 표시로 방위를 쉽게 알 수 있게 합니다.

군대나 선박 등에서 활용하고 진행 방향 또는 지금 바라보고 있는 단위로합니다.

각도가 시간과 겹치게 되면서  1분은 1'이라고 쓰고 1/60˚, 1초는 1"라고 쓰고 1/3600˚(도)가 됩니다.

이 분과 초 단위는 정밀한 가공이나, 우주단위의 연구에서 많이 사용하고 있습니다.

그리고 마지막으로 라디안 단위를 많이 사용합니다.

같은 각도일 때 반지름이 길어지면 호도 길어지는 어떤 비율이 존재하는데 ,

반지름(R)과 호의 길이(L)와의 비율인 L / R가 라디안입니다.

차원은 (길이) / (길이)임으로 없고, 단위를 표시할때는 rad라고 표기합니다.

이 라디안의 특성은 180˚ = π rad ( 3.14 rad )라는 것입니다.

그래서 90˚ = π / 2 rad, 60˚ = π / 3이 됩니다.

그리고 일반 각도 단위를 라디안으로 변경할 때는 rad = 도 x π /  180 이라고 하면 됩니다.

라디안을 사용하는 이유는 편리하기 때문입니다.
일단 개념적으로 호와 반지름의 길이의 비이기 때문에 단위가 없어 계산값에 영향이 없습니다.
그래서 많은 물리공식들에서 사용하기를 선호되며 그에 따라 공식들도 깔끔하게 적용됩니다.

360도와 라디안으로 나타냈을때 공식의 차이를 보겠습니다.

다만 라디안도 단점이 있는데 π(파이)가 들어가다 보니 기본적으로 값이 무리수입니다.

우리는 일상에서 90도가 직각이고 45도 하면 어느정도인지 대충 알고있습니다.

특히 직업적으로 구조를 다루게 되면 15, 30, 45, 60, 90, 180, 270, 360도는 많이 쓰는 각도이고요.

라디안은 이런점에서 직관적으로 90˚ = 3.14 rad라고 해도 알아 듣기가 어렵습니다.

실생활에서 쓰기 어렵다는 것이죠.

엑셀에서는 RADIANS 함수를 사용하면 도단위를 라디안 단위로 변환합니다.

그리고 DEGREE 함수를 사용하면 라디안 단위를 도 단위로 다시 변환할 수 있습니다.

RADIANS(angle) : 360도로 나타내는 각도를 라디안 단위로 변환합니다.

Degree(rad) : - π ~ π로 각을 표현하는 라디안 단위를 도로 변환합니다.

하지만 오히려 직접 연산하는게 좀 더 편할수도 있습니다.

degree 함수를 직접 계산하면 아래와 같이 됩니다.

저는 일상적인 각도는 라디안으로는 감이 잘 안와서 역변환을 자주 사용합니다.
그래서 이 공식은 외우고 다니게 되더라고요.

목차

1. 제곱과 제곱근

2. 제곱근의 의미

3. 엑셀에서 제곱근 구하는 법

1. 제곱과 제곱근

수학은 사칙연산 +, -, ÷, ×으로 시작됩니다.

여기에 한단계 나아가면 제곱이 나옵니다.

제곱은 같은 수를 거듭해서 곱하는 것입니다.

두번 곱하는것을 제곱, 3번은 세제곱, 4번은 네제곱이라고 할 수 있고 수가 커지면 n승이라고 읽습니다.

• 2의 제곱 2 × 2 = 4
• 2의 세제곱 2 × 2 × 2 = 8
• 3의 4승 3 × 3 × 3 × 3 = 81

손으로 쓸때는 3² (3의 제곱), 10⁸ (10의 8승) 라고 해서 숫자 위에 작은 숫자를 써서 표시합니다.

컴퓨터에서는 프로그램마다 다르지만 거의 대부분 ^ 연산자를 주로 사용합니다. 

10 ^ 5 는 100,000이니 간단하게 큰수를 표현할 수 있는 개념입니다.

이 제곱을 꺼꾸로 하면 제곱근이라는 개념이 됩니다.

• 2를 제곱하면 4가 되니 4는 2의 제곱근이고, 같은 방식으로 9는 3의 제곱근입니다.

• 2를 세제곱하면 8이니, 8은 2의 세제곱근이고, 같은 방식으로 27은 3의 세제곱근입니다.

이걸 표기로는 √ 라고 표기하고 루트라고 읽습니다.

세제곱근 ∛, 네제곱근은 ∜으로 표기앞에 3, 4를 입력하지만 생략하면 2 제곱근으로 봅니다.

2. 제곱근의 의미와 활용

피타고라스의 법칙이라고 유명한 공식은 아래와 같습니다.

각변으로부터 사각형의 대각선을 읽는 이 공식은 삼각형의 빗변의 길이를 구하는데 잘 알려져 있습니다.

피타고라스 학파라고 불리는 전설적인 그리스 시대의 집단은 학파이지만 사실상 수학을 기점으로 하는 종교집단입니다.

비밀결사에 가까운 사람들은 이 공식을 굉장히 중요한 비밀로 생각했다고 합니다.

이 걸 연구하다 처음 root(2)의 존재를 알게 되었고 무리수가 세상에 나타나게 되었다는 유명한 이야기가 있습니다.
히파소스라는 사람이 이걸 세상에 알리려다가 암살당했다는 이야기가 전설처럼 내려옵니다.

왜 대각선을 구하는게 중요하냐면 2차원 도형은 구를 제외한 모두 삼각형으로 나타낼수 있습니다.
구조를 직각 삼각형의 합으로 구할 수 있다는 것이죠. 반대로 말하면 직각삼각형으로 쪼갤 수 있습니다.
심지어 원형도도 삼각형의 집합으로 근사킬 수 있습니다.

거리를 계산할때는 물론이요, 높이를 계산할 때도 편리한 공식입니다.

예를 들어 건물을 지을 때 보강 구조물의 길이를 구할때는 가로와 세로 높이로 대각선의 길이를 구하면됩니다.

또 산의 높이를 구할때 삼각거리법을 사용할 수 있습니다.

실제로 산의 높이는 대지거리와 대각선 거리를 구하고 높이를 계산합니다.

너무 높은 산은 아래 과정을 연속으로 실행합니다.

3. 엑셀에서 제곱근 구하는 법

엑셀에서 구하는법은 SQRT라는 함수와 지수연산자 ^를 이용하면됩니다.

먼저 SQRT를 살펴보겠습니다.

SQRT(number) : number의 제곱근을 구합니다. n ^ (1/2)와 결과가 같습니다.

함수로 SQRT가 있지만, ^연산자로도 계산이 가능합니다.

n에 1/2인 ^ 연산자로 계산하면 제곱근이 됩니다.

n^(1/2) 는 제곱근이고 n^(1/3)은 세제곱근입니다.

그런식으로 여러가지 근을 적용할 수 있습니다.

엑셀을 전문적인 수학툴로 쓰기에는 조금 부족한 면이 있지만, 어느정도라면 사용가능합니다.

있어서 나쁠 것이 없죠.

목차

1. 모집단, 표본집단 왜 나누어야 하죠?

2. 표준편차의 활용

3. 표본집단의 표준편차(n-1 방식)의 의미

4. 표본집단의 표준편차(n-1 방식)의 한계와 극복하기

 
 
표준편차의 뜻과 계산에 대해서 지난번에 포스팅 했습니다.
표준편차는 의미는 쉽지만 사용함에 있어 설명을 추가로 필요합니다.
표준편차의 의미와 계산하는 방법은 아래링크를 참고하세요.

오늘은 모집단과 표본집단에 대해서 좀 더 자세히 알아보고 그 활용을 알아보고자 합니다.
두 개의 표준편차 공식이 달라 모집단의 표준편차 계산방식은 (n 방식), 표본집단은 (n-1 방식)이라고 설명하겠습니다.

※ 이번 포스팅은 이론적인 면도 있지만 제 경험과 의견을 기반으로 함을 미리 알려드립니다.
 

1. 모집단, 표본집단 왜 나누어야 하죠?

 
모집단은 대상의 모든 데이터이고 표본집단은 데이터의 일부만 조사한 경우입니다.
따라서 표본집단은 모집단의 안에 포함된다고 볼 수 있겠네요.

모집단의 경우에는 데이터를 전수조사한 경우입니다. 모집단이 보통 같지만 오히려 표본집단을 많이 씁니다.
왜냐면 모든 사건이 일어났는데 분석하는 건 늦었을 때가 많기 때문이죠. (그래도 어느정도는 사용합니다.)
비교적 표본집단의 데이터만 얻게 되는 경우가 더 많습니다.
 

1.  모집단 전체의 데이터를 얻기에는 너무 많고 조사하는데 시간이 많이 필요한 경우
     예) 한국인 모두의 설문조사
2.  데이터가 시간에 의해 발생하는데 미래의 데이터를 미리 측정할 수 없는 경우
     예) 수요일의 사당역 이용자수 - 다음주 수요일이 항상 존재함으로 지금까지 데이터를 전부라고 할 수 없습니다.
3.  데이터를 측정하는데 시료가 파괴되는경우
     예) 휴대폰 새로운 모델 액정의 파열강도 - 시료를 전부 검사하고 나면 사용할 다른 시료를 만들어야 합니다.

 
가만 생각해보면 거의 모든 경우에는 모집단 이란 건 없는 거나 다름없죠.
미래에 생길 일까지 포함하면 전부 측정하는 것은 불가능합니다.
그래서 표본집단을 분석하는게 도움이 됩니다.
 
 

2. 표준편차의 활용

 
아래의 그래프에서 A는 산포가 넓고, B는 산포가 좁습니다.
그래프 안의 빨간 점선이 기준일 때  A그래프의 산포군에서는 점선을 넘는 데이터가 발생하고,
B 그래프에서 가망이 없어 보입니다.(확율이 너무 낮아서 0이나 다름 없든지)
 

표준편차를 알면 과거 시점 혹은 다른 곳에서 측정한 데이터를 기반으로 사건이 일어날 확율을 미리 예상 할 수 있습니다.
정규분포에서는 표준편차의 3배가 넘어는 경우 0.3%이하 표준편차의 6배가 넘는 일은 0.0004% 이하로 떨어진다고 합니다.
산포의 모양이 정규분포만 있는건 아니지만 대략적으로 표준편차의 배수로 예상할 수 있습니다.
 

3. 표본집단의 표준편차(n-1 방식)의 의미

 
모집단의 표준편차(n방식)은 사전적인 의미 그대로 입니다.
중요한건 표본집단의 표준편차인데요. 수학적인 증명은 하지 않고 설명만 드리겠습니다.
 

1. 아래 그림처럼 커다란 모집단에서 표본집단을 한번 측정한다고 하겠습니다.
2. 만일 이 표본집단을 여러번 측정한다면 모집단의 크기에 점점 가까워집니다.
3. 이 상황을 수학적으로 전개하면 표본집단을 무수히 측정했을때 그 값은 n-1 방식에 수렴합니다.
   (적은 수로 실험해도 반복하면 표준편차는n-1방식에 접근합니다.)

 
"n-1 방식 - 표본집단 표준편차는 집단의 일부로 전체 표준편차를 예상한 것"입니다.
 

 4. 표본집단의 표준편차(n-1 방식)의 한계와 극복하기

 
툭하면 일기예보는 안맞고 아무리 전문가라도 주식은 다 틀립니다.
이제 표준편차라는 강력한 도구가 있는데 어째서 한계가 있을까를 알아야 합니다.
예측은 예측일 뿐이라는 편안한 표현으로 넘기지 말고 원인을 공부해서 대책을 세워 봅시다.
 

① 데이터가 집단을 대표할 수 없을때
 
예를 들어 출퇴근 시간에 대해서 조사를 해 보겠다고 하겠습니다.
하기를 보면 표본집단이 하나의 요소(교통수단) 쏠려 전혀 집단을 대표하지를 못합니다.
 

② 극복하기 위해 데이터의 대표성을 확보하기
 
이런 경우에는 데이터를 조사할 때 오른쪽처럼 되도록 강제로 유도할 필요가 있습니다.
유도하려면 인자를 잘 알고 있어야 할 것입니다.
자동차를 타는 사람과 자건거를 타는 사람들을 똑같은 수로 모으면 데이터의 대표성이 향상됩니다.
 

③ 데이터는 결국 많을 수록 믿을 만합니다.
 
위는 극단적이고 살짝 현실적으로 생각해 보겠습니다.
보통의 경우 현상이란 통제가 어려운 인자 여러개가 작용한 결과입니다.
따라서 우리는 표본집단이 충분히 제어되는지 알기 어렵습니다.
그럴때는 오른쪽 처럼 많이 조사 집단을 크게 하는 것이 답이 될때가 많습니다.
무식하다고 생각하실지 모르지만 이런 경우에는 양으로 밀어 붙이는게 현장에서 가장 잘 쓰는 방법입니다.
 

④ 표준편차를 사용할 수 없을 때 - 데이터가 불연속 적일때
 
인자의 데이터가 불연속 적인 경우가 있습니다.
이런 경우에는 표준편차의 적용이 어렵습니다.
 

예를 들어 습도는 어느이상 포화되면 이슬이 맺이게 됩니다.
정밀한 화학 실험에서는 포화 전후가 완전히 다른 양상을 보이게 될 것입니다.
그 외에도 일반적인 사물이 깨지는 현상, 얼거나 기화되어 상이 변할 때 등등 연속적이지 않은 현상이 있습니다.
사실 이런 경우에도 여러가지 해결방안이 있습니다.
구간을 나누거나 다른 지표를 사용해서 대체 하거나 하는 방법으로 컨트롤 합니다.
이건 여러분야에서 연구됩니다. 주식에서  갑작스러운 적대적 M&A, 날씨에서는 가까운 곳에서
화산 폭발처럼 갑작스러운 현상들을 예측하려 노력하는 사람들이 있습니다.
불연속적인 데이터를 관리하는 정규적이지도 않고 요령과 감이 필요하며 내용도 너무 깁니다.
다음에 기회가 된다면 소개하고 싶네요.
 

⑤ 표준편차를 사용할 수 없을 때 - 예상을 뛰어 넘을 때
 
예상을 뛰어넘을 때라고 말할수도 있고 비선형성이 너무 심할때 라고 표현할 수 있습니다.
현실에서는 정규분포에서 벗어난 인자가 그 동안 관측되지 않았지만 오늘 처음 일어난 인자가 존재합니다.
그 인자가 너무 비선형적이라면 예측이 지극히 어렵습니다.
아래 그래프의 빨간 박스영역을 관측하고 그 외의 영역을 예상하는 건 거의 불가능 할 것입니다.

이런 경우도 이론만 따지면 수학적으로는 대응이 가능합니다.
하지만 현실적으로 예상해서 움직이기가 어려운 케이스라고 볼수 있습니다.
(시물레이션 모델이 우수하다면 알아낼지도 모르죠.)
 
 

4. 데이터는 얼마나 확보를 해야 하나요?

 
우리는 산포와 예측에 대해 고민하보면 결국 이 질문에 도달합니다.
통계학적으로 n>=30개 이면 유의미한 데이터를 얻을 수 있다고 합니다.
하지만 현실적으로 여러 인자들에 의해 표본집단에 대해 보장을 할 수 없어 30개로 부족합니다.
그렇다고 무작정 많이 하라는 것은 아닙니다. 가능한 인자를 제어하는 게 중요합니다.
예로 기계(인자)가 여러 대 일 경우 3대 이상을, 다수의 사람들이 만드는 패턴이라면 최소 주말과 평일을 나누어서 데이터를 수집해야 합니다.
최대한 다양한 데이터를 얻는 것이 미래의 사고를 예방할 수 있습니다.
 
그러나 도무지 비용적인 한계가 있는 경우가 있습니다.
그럴 때는 이론과 모델링을 통해서 피해를 최소화하며 검증해야 하겠죠.
가능하기는 하지만 통계를 통해 미래를 예측하는 것은 어렵습니다. 저 역시 현실의 비용과 시간한계속에서 시험의 양과 인자를 제어하는 건 항상 시행착오가 있습니다.
 

여기까지 표준편차의 통계적인 활용과 한계에 대해서 설명드렸습니다.
늘 안타까운게 기술 개발 현장에서 개인적은 생각은 교육을 많이 받는 사무직 직원들은 정말 통계값을 잘 활용하지만,
비교적 현장 관리자들은 공식만 보고 겁을 먹고 공부도 잘 하지 않는 것 같습니다.
현실적으로 통계학이론으로 한계가 있는 점은 많지만 그래도 잘 알고 활용한다면 강력한 툴이됩니다.
한 사람이라도 도움이 되기를 바라며 포스팅 해 보았습니다.